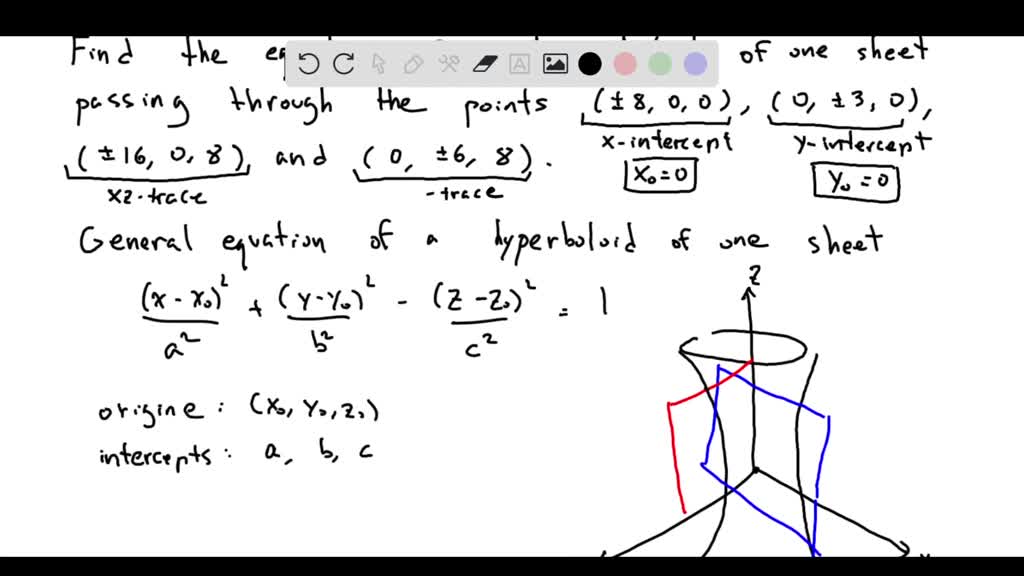
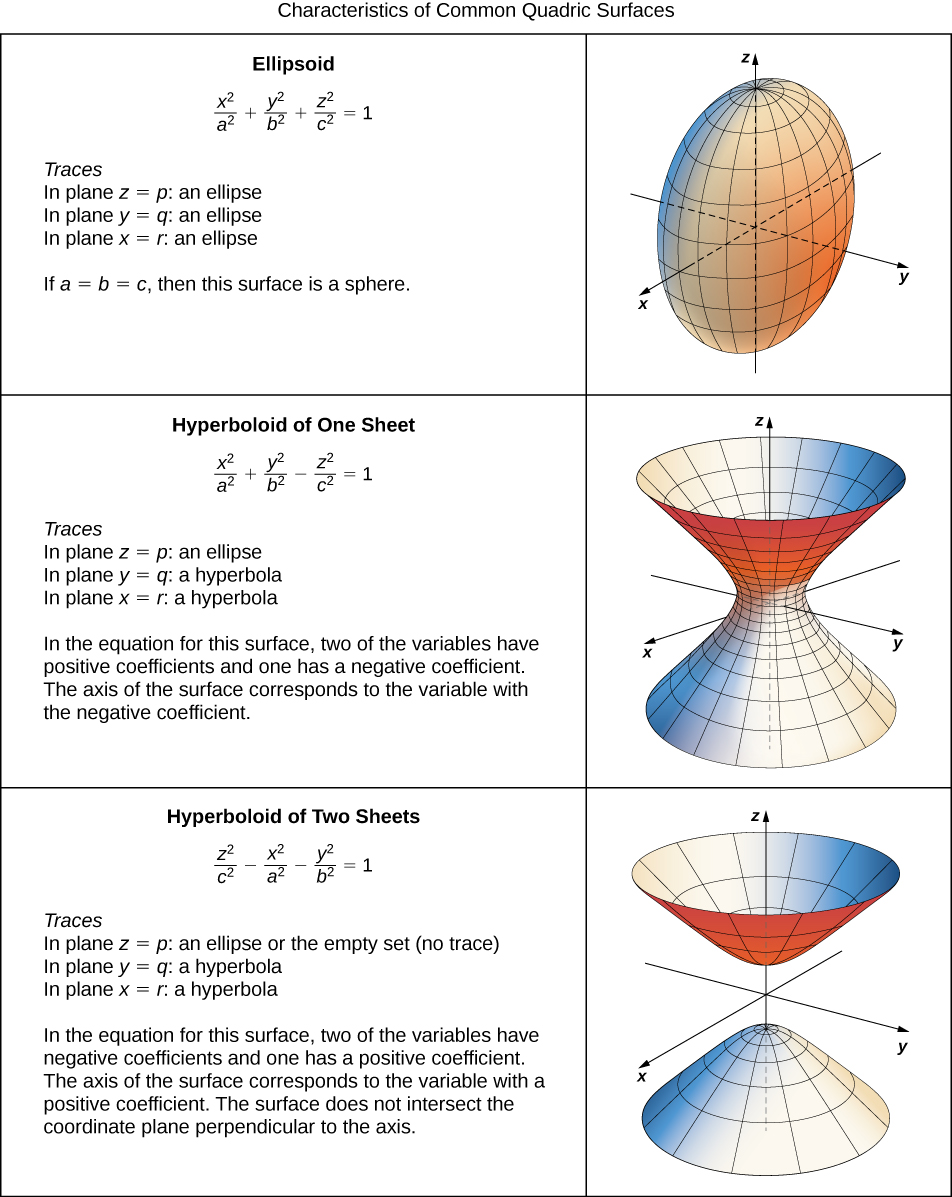
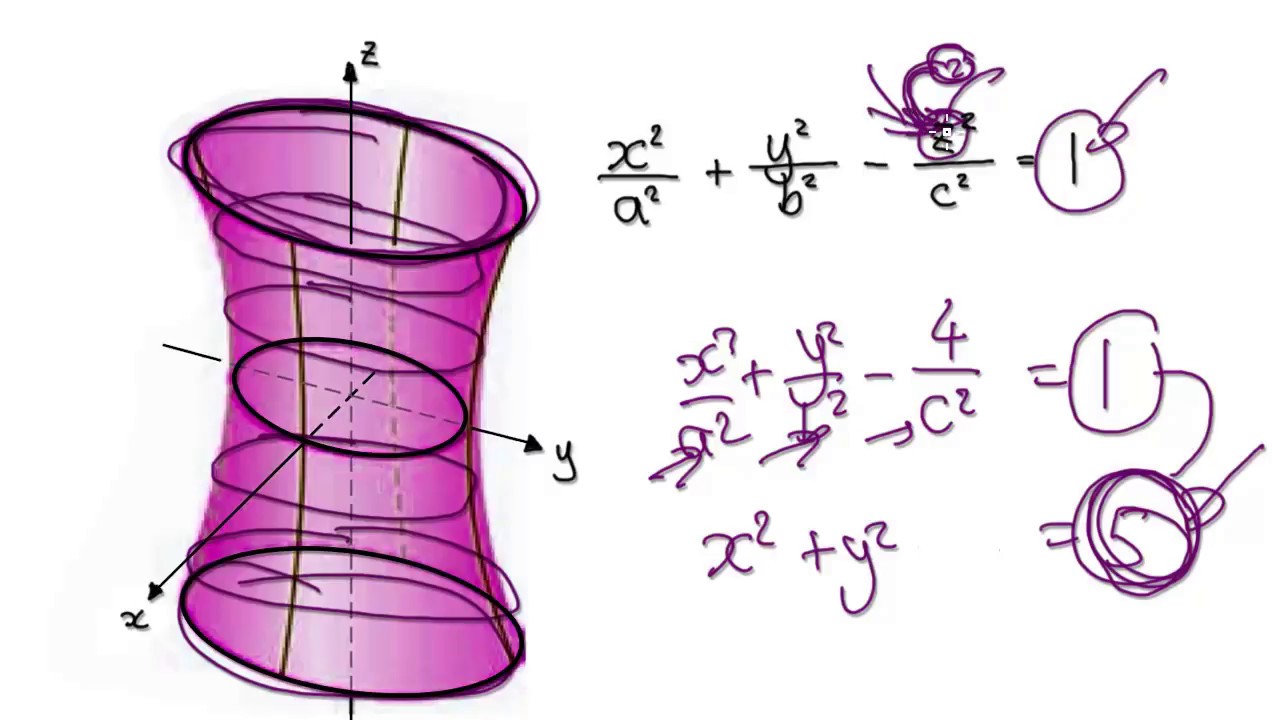
Hyperboloid Of One Sheet Equation - A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower.
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Solved Consider the hyperbolic paraboloid. Give the equation
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
SOLVED Find the equation of the hyperboloid of one sheet passing
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Quadric Surfaces · Calculus
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Quadric Surface The Hyperboloid of Two Sheets YouTube
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Quadric Surface The Hyperboloid of One Sheet Vector Calculus YouTube
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower.
Graphing a Hyperboloid of One Sheet in 3D YouTube
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Video 2962 Calculus 3 Quadric Surfaces Hyperboloid of one sheet
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower.
Solved For the given graph of a hyperboloid of one sheet
Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Quadric Surfaces (Identified and Explained w/ Examples!)
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower.
Chapter 12Section6 Quadric Surfaces ppt video online download
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Learn about the equation and cross sections of a hyperboloid of one sheet, a quadric surface that resembles a cooling tower.
Learn About The Equation And Cross Sections Of A Hyperboloid Of One Sheet, A Quadric Surface That Resembles A Cooling Tower.
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).